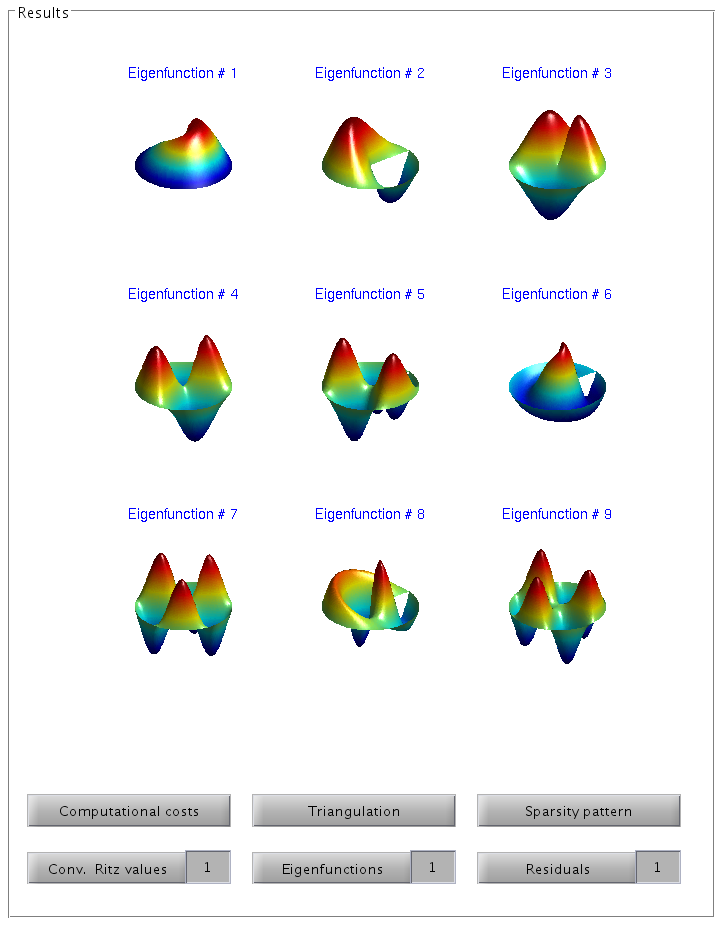
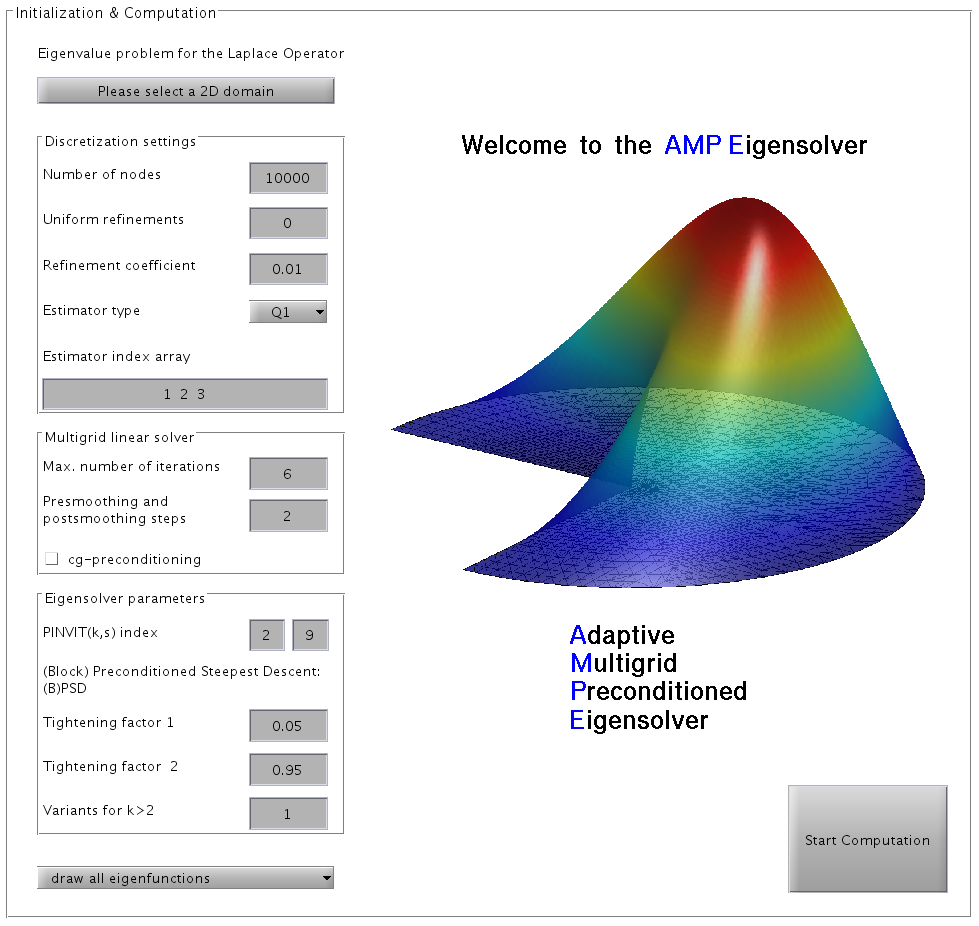
AMP Eigensolver

Adaptive Multigrid Preconditioned Eigensolver,
Version 1.0, July 2014.
Authors: Ming Zhou and Klaus Neymeyr at the Universität Rostock, Institut für Mathematik, Germany.

The AMP Eigensolver (Adaptive Multigrid Preconditioned Eigensolver) is a software for computing the smallest eigenvalues and the associated eigenfunctions of a self-adjoint and elliptic partial differential operator in 2D domains. The AMP Eigensolver software contains a fast adaptive grid refinement and an efficient iterative eigensolver with multigrid preconditioning. The adaptive grid refinement uses residual based error estimators with respect to linear and quadratic finite elements. The eigensolver is an implementation of the preconditioned gradient subspace iteration for the Rayleigh quotient. The preconditioner is a multigrid V-cycle with Jacobi smoothing. See [9] for numerical experiments with the AMP Eigensolver.
The core of the software is written in FORTRAN and uses the BLAS and LAPACK libraries. The FORTRAN code has been precompiled for the following platforms:

The users' front-end is a graphical user interface (GUI) in Matlab.

Download of the AMP Eigensolver:

References:

  1. Z. Bai, J. Demmel, J. Dongarra, A. Ruhe, and H. van der Vorst, editors. Templates for the solution of algebraic eigenvalue problems: A practical guide. SIAM, Philadelphia, 2000.
  2. E. G. D'yakonov. Optimization in solving elliptic problems. CRC Press, Boca Raton, Florida, 1996.
  3. W. Hackbusch. On the computation of approximate eigenvalues and eigenfunctions of elliptic operators by means of a multi-grid method. SIAM Journal on Numerical Analysis 16 (1979), 201-215.
  4. A. V. Knyazev. Toward the Optimal Preconditioned Eigensolver: Locally Optimal Block Preconditioned Conjugate Gradient Method. SIAM Journal on Scientific Computing 23 (2001), 517-541.
  5. A. V. Knyazev, M. E. Argentati, I. Lashuk and E. E. Ovtchinnikov. Block Locally Optimal Preconditioned Eigenvalue Xolvers (BLOPEX) in hypre and PETSc. SIAM Journal on Scientific Computing 29 (2007), 1267-1280.
  6. A. V. Knyazev and K. Neymeyr. A geometric theory for preconditioned inverse iteration. III: A short and sharp convergence estimate for generalized eigenvalue problems. Linear Algebra Appl. 358 (2003), 95-114.
  7. D. E. Longsine and S. F. McCormick. Simultaneous Rayleigh-quotient minimization methods for Ax = λBx. Linear Algebra Appl. 34 (1980), 195-234.
  8. K. Neymeyr. A posteriori error estimation for elliptic eigenproblems. Numer. Linear Algebra Appl. 9 (2002), 263-279.
  9. K. Neymeyr and M. Zhou. The block preconditioned steepest descent iteration for elliptic operator eigenvalue problems. Electron. Trans. Numer. Anal. 41 (2014), 93-108.

Two screenshots of the AMP Eigensolver:

License information:

The software AMP Eigensolver is an eigensolver for self-adjoint and elliptic partial differential operators in 2D domains.
© 2014 Ming Zhou & Klaus Neymeyr, Universität Rostock, Institut für Mathematik.

The software can be used for academic, research and other similar noncommercial uses. The user acknowledges that this software is still in the development stage and that it is provided by the copyright holders and contributors "as is" and any express or implied warranties, fitness for a particular purpose are disclaimed. In no event shall the copyright owner or contributors be liable for any direct, indirect, incidental, special, exemplary, or consequential damages.

The copyright holders provide no reassurances that the source code provided does not infringe any patent, copyright, or any other intellectual property rights of third parties. The copyright holders disclaim any liability to any recipient for claims brought against recipient by any third party for infringement of that parties intellectual property rights.

The user has to respect the LAPACK license, see http://www.netlib.org/lapack/LICENSE.txt.