Practical exercise:
Numerical solution of a differential equation with the Picard iteration. Infection modelling and stability analysis of the model.
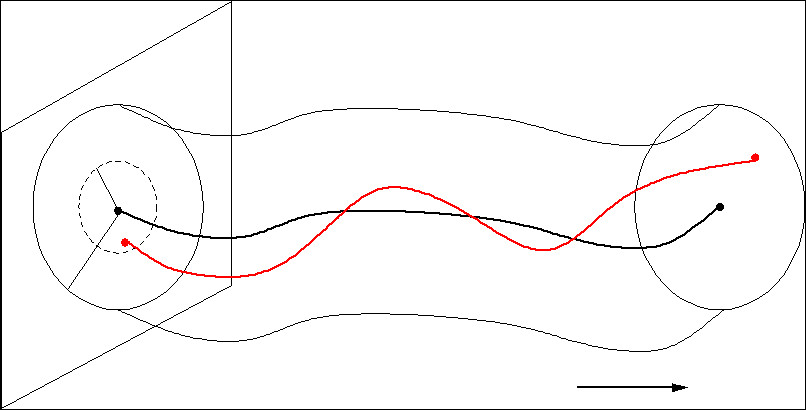
Lyapunov stability
Top| This summer school will give a unique introduction into modelling with differential equations combined with data analysis. This includes both deterministic dynamical systems theory as well as stochastic systems. Lectures will cover mathematical techniques for analysing complex systems of various fields in science and engineering. All theoretical parts of the course will be accompanied with hands on exercises using real life examples ranging from mechanics over medicine to economy. |
|
Important examples of differential equations in
science and engineering, mathematical modelling,
elementary solution methods, existence and
uniqueness, numerical solutions, phase space,
Lyapunov stability, asymptotic stability and
Lyapunov functions. |
|
Practical exercise: Numerical solution of a differential equation with the Picard iteration. Infection modelling and stability analysis of the model. |

Lyapunov stability Top |
| Runge-Kutta methods for non-stiff and stiff
systems, error estimation, adaptive step size
control, sensitivity equations, dynamic optimization,
parameter estimation and
optimal control. |
|
Practical exercise: Optimal control in an artificial pancreas for type 1 diabetics. |
 Control of glucose level Top |
| Stable manifolds, unstable manifolds, center
manifolds, homoclinic orbits, heteroclinic orbits and
center manifold reduction. |
|
Practical exercise: Sensitivity of dependence on initial values in a chemical reaction. |
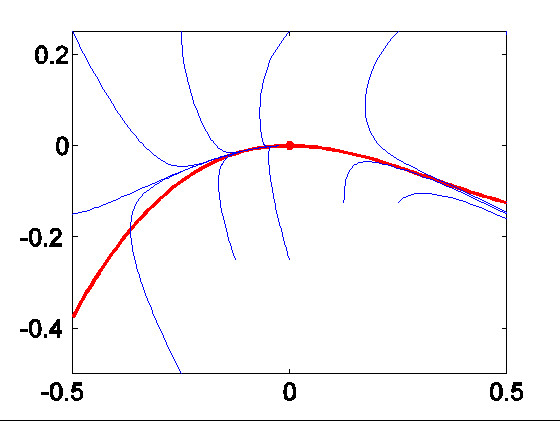 Center manifolds reduction Top |
| Theorem of Poincaré-Bendixon, Poincaré-sections,
stability of periodic orbits and forced oscillators. |
|
Practical exercise: Modelling a swing; analysis of the Mathieu equation. |
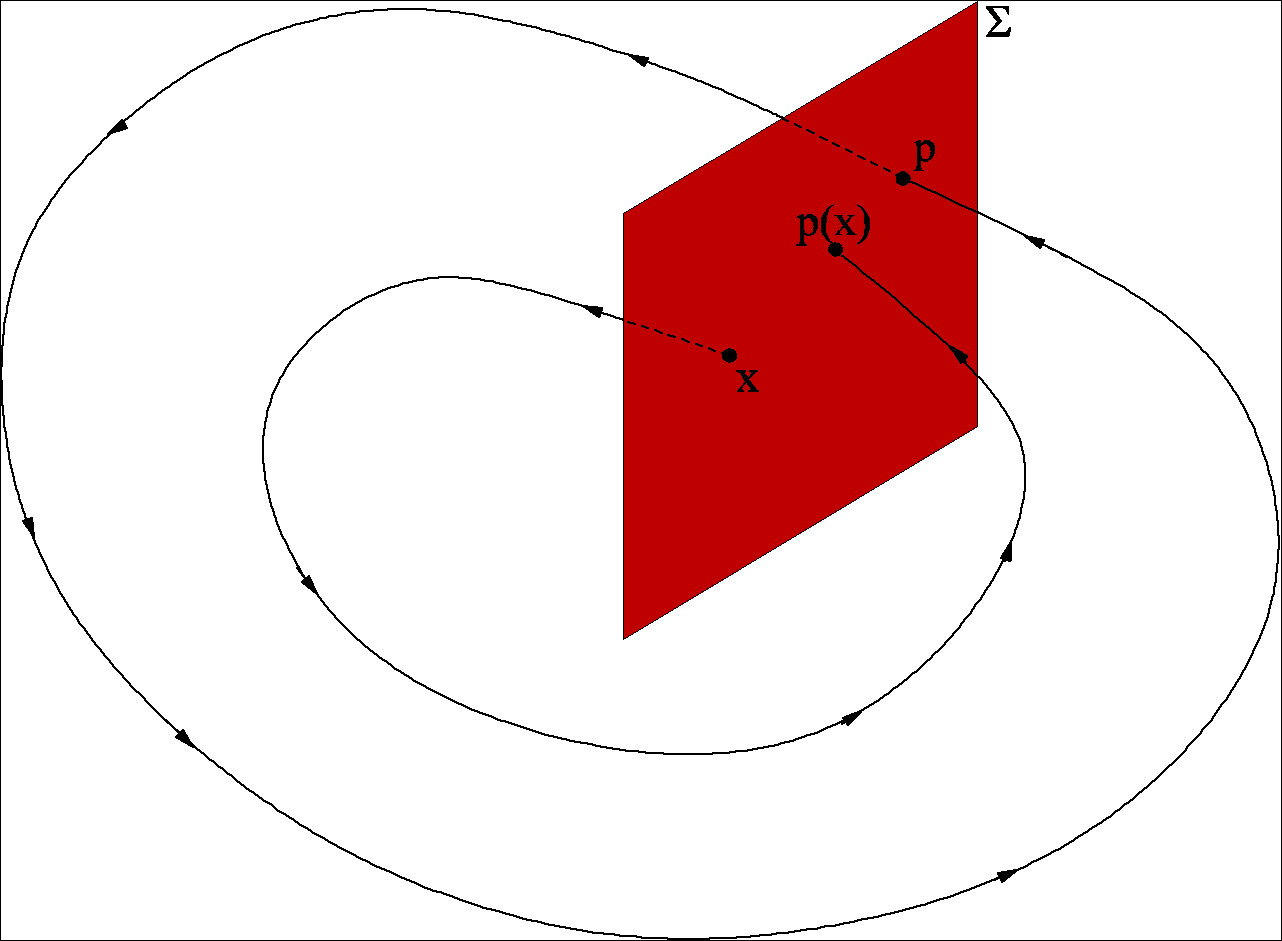 Poincaré maps Top |
| Implicit function theorem, structural stability,
saddle-node bifurcation,
transcritical bifurcation,
pitchfork bifurcation,
Hopf bifurcation and
continuation techniques. |
|
Practical exercise: Modelling an electric circuit and Van der Pol oscillator. |
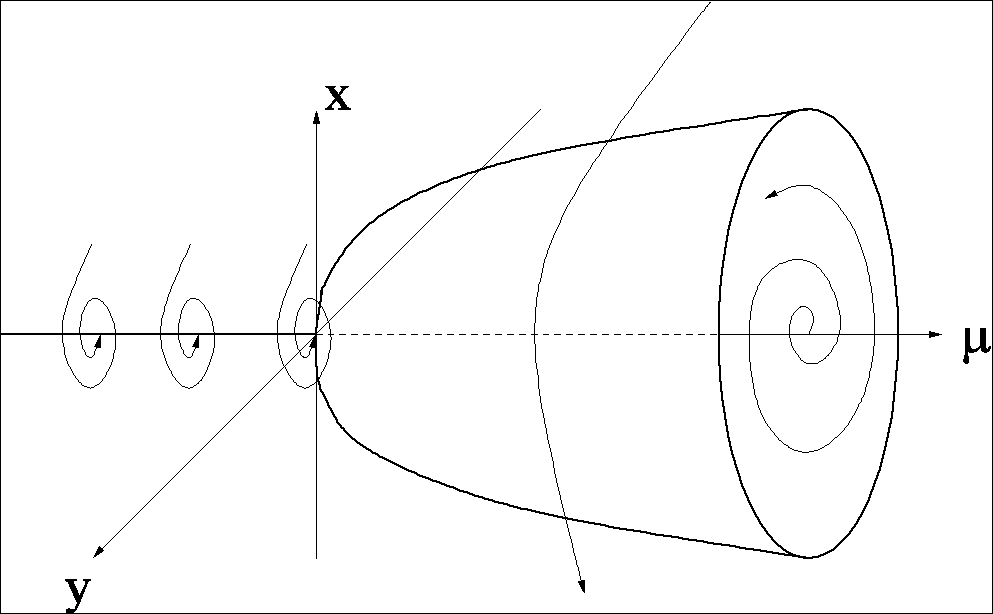 Hopf bifurcation Top |
| Characteristics for time series, parametric and nonparametric modelling,
models for linear and nonlinear time series, model identification, estimation
and verification, predictions in time series.
Practical exercise: Prediction of bond prices. |
|
Practical exercise: Prediction of bond prices. |
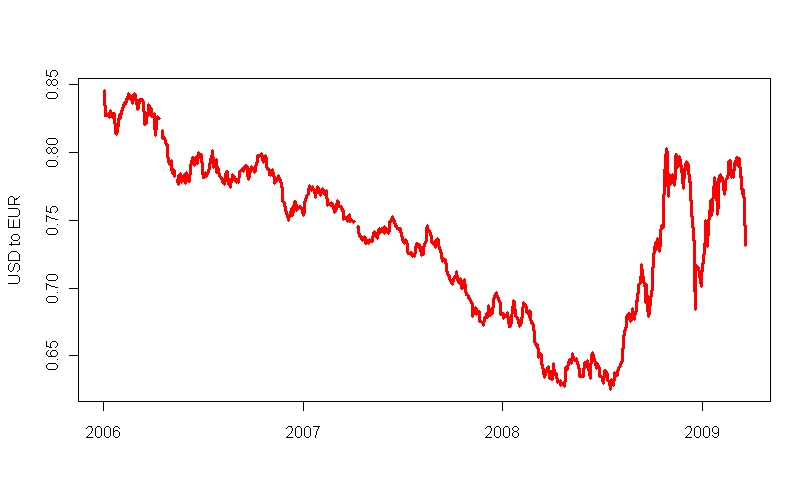 Bond prices overtime Top |
| Introduction to stochastic differential equations, Itô
and Stratonovich integrals, grey-box modelling,
parameter estimation and model building. |
|
Practical exercise: Stochastic modelling of the insulin glucose relation. |
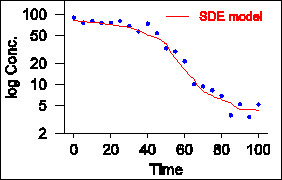 Parameter estimation for SDE model Top |
| Nonlinear partial differential equations, travelling
waves and soliton solutions, Korteweg de Vries
equation, complex pattern formation in reaction
diffusion equations, reduction to systems of
ordinary differential equations, homoclinic and
heteroclinic connections. |
|
Practical exercise: Spiral waves in the Belousov-Zhabotinsky reaction. |
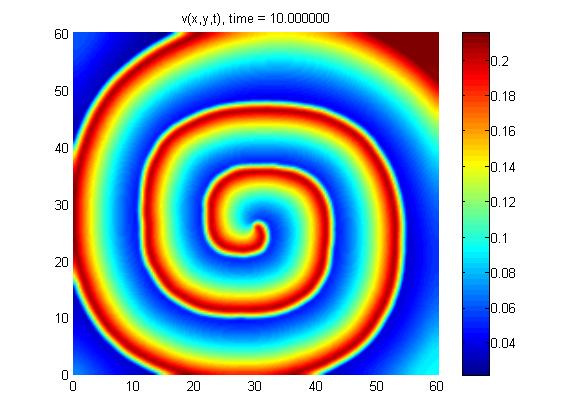
Pulse propagation in form of spiral vawes Top |
created by: Gabriella Keuer
last updated: March 15, 2018